Do the Math on the Mind

Can Mathematics Understand the Brain?

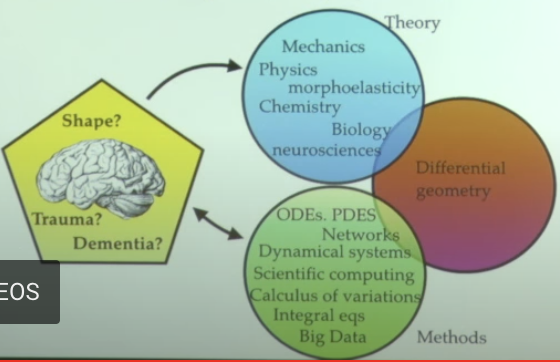
Alain Goriely is a professor of mathematical modeling at the Oxford Mathematical Institute, with a research focus on the human brain and its development. He has primarily studied morphogenesis in the brain, and in the video above, he explores the brain from the perspective of industrial and applied mathematics. Specifically, the video covers (1) the scaling laws of weight and cortical surface area in the brain, (2) modeling cortical folding patterns through morphogenesis, (3) solving issues related to hydrocephalus and brain edema, and (4) offering new insights into neurodegenerative diseases through diffusion modeling based on brain network models.

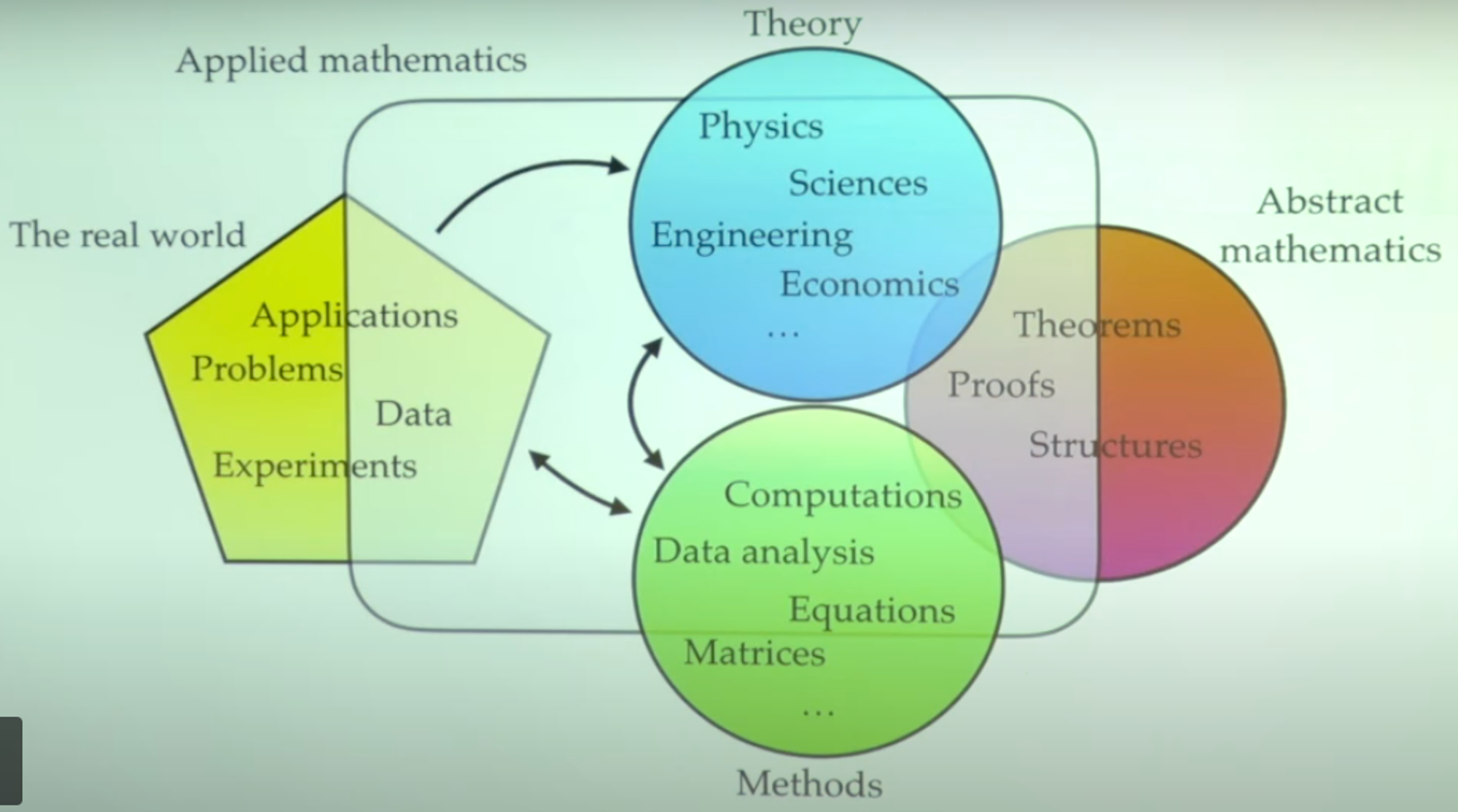
Goriely’s perspective on applied mathematics is particularly fascinating. He explains that applying abstract mathematics to real-world problems involves both theory and method. For example, methods may include equations, matrices, data analysis, and computational algorithms, while theories may draw on established frameworks from physics, science, engineering, and economics. According to Goriely, applied mathematics is about appropriately setting theory and methods through abstract mathematics to solve practical problems.

---

So how should we approach the practical challenge of developing a brain theory that explains human phenomenological consciousness? We cannot fully capture experiential information through experiments alone. However, by leveraging communication and introspective descriptions from subjects, we can obtain data, and through imaging, we can observe the neural activities corresponding to these experiences. What kind of mathematics should we employ, and what theories and methods should we apply in modeling this? Such questions may seem futile without considering potential answers. In other words, if we do solve this problem, what would that allow us to achieve?

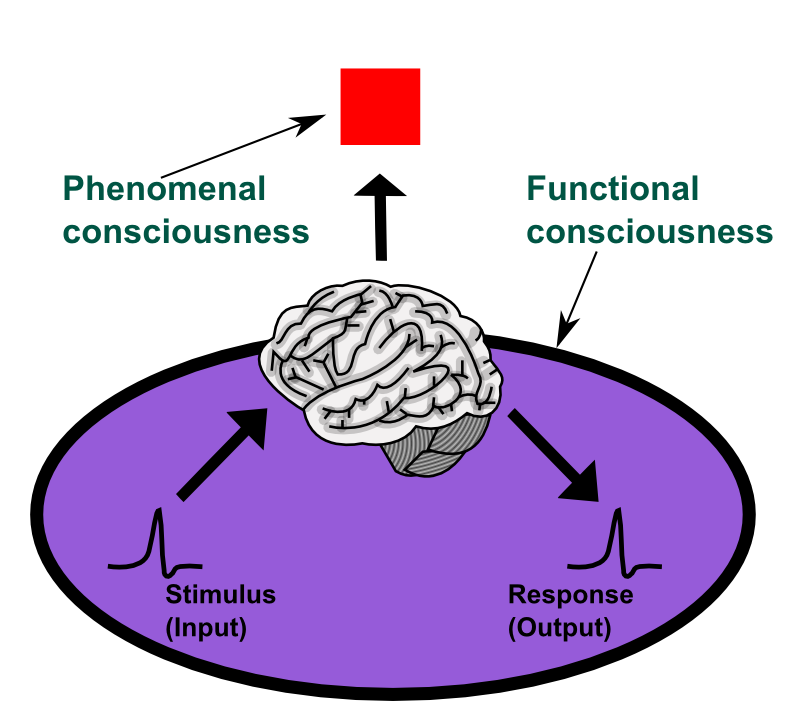
The Australian philosopher David Chalmers once defined problems related to human phenomenological consciousness as either the “easy problems,” concerning how the brain perceives, recognizes, learns, and acts, or the “hard problem,” concerning why and how these processes are connected to consciousness. The problem we’ve defined differs somewhat from these categories. We approach it from a more scientific perspective rather than a metaphysical one. In this context, our earlier question challenges the possibility of developing a theory that biologically explains, predicts, and controls phenomenological consciousness and experience. This falls under Anil Seth’s “Real Problem,” aiming to mathematically describe (Dynamic), analyze (Mechanic), and explain (Principle) the fundamental workings of conscious content and states.

---

Future

What does it mean to mathematically describe the state of consciousness? Consider how we describe the state of motion in mechanics. We use variables like position, velocity, and acceleration to describe the center of mass and point masses, or we introduce the concept of energy to derive results when describing the motion of an object. Similarly, in statistical mechanics, we describe the state of a gas by using statistical properties such as temperature, pressure, and volume, rather than describing each gas molecule individually. This approach to description establishes the core terms of a theory for the state of the physical system being described. It also provides conversion rules between different perspectives, helping to align different understandings of a common subject. This descriptive approach may be inherently perspectivist and social in nature.

Questions

• What are the key physical variables needed to describe the state of consciousness?
• What characteristics do these variables possess?
• Are there logical rules these variables must satisfy? In what mathematical space should the theory be developed?
• What are the most effective ways to visualize this information?

What does it mean to explain the state of consciousness? In mechanics, to explain the motion of an object, we must present causal relationships between the variables involved. In statistical mechanics, to explain the state of a gas, we consider the statistical causality among the statistical variables to present the relationships between past, present, and future states. This explanation involves establishing causal or quasi-causal relationships among the variables we’ve refined and using these to derive new knowledge. It involves reasoning, using methods such as deduction, induction, and abduction. The content of such explanations should effectively answer related questions like:

Questions

• Can the presence or absence of consciousness be verified or quantified?
  • Consciousness in animals/machines
• Can the content of consciousness be expressed or compared?
  • Comparing one’s own conscious content
  • Comparing one’s conscious content with that of others
  • Comparing oneself with objects/others
• Can we upload/download parts or all of our consciousness to/from a computer?