인공지능 vs 두뇌
“우리에게 너무나 어려운 문제들, 인공지능은 어떻게 풀어내는가? 우리에게는 너무나 쉬운 문제들, 인공지능은 왜 못 풀어내는가? 인공지능의 관점에서 바라보는 인간지능이란 무엇인가?”
본 글은 이상완 교수님께서 저술하신 “인공지능과 뇌는 어떻게 생각하는가[1]”를 읽고 정리한 글입니다.
1. 무한한 세상을 유한한 공간에 담다
해당 챕터는 사과를 어떻게 인식Recognition하는지, 연관짓기 문제Binding Problem를 중심으로 추상화와 다양성의 딜레마를 소개한다. 이를 해결하기 위한 초기 인공지능 연구의 역사적 흐름을 소개한다. Marvin Minsky의 Feedforward Network에서 시작한 추상화 과정과, 여기서 발생하는 Credit Assignment Problem을 해결하기 위한 Error Backpropagation 알고리즘을 소개한다.
2. 현재의 성공이 미래의 실패가 되다
첫번째 챕터에서는 단순히 주어진 현재의 문제에 집중했다면, 두번째 챕터는 현실 상황에서 상호작용하는 통계적 상황에 집중한다. 통계적 기계학습의 관점에서 Structural Risk Minimization을 소개하며, Underfitting/Overfitting을 막기 위한 Tikhonov Regularization 방법을 소개한다. 더 나아가, Dual Problem을 생각하여 Support Vector Machine(SVM)을 소개한다.
Bias-Variance Tradeoff를 해결하기 위해 채택한 “모델의 효율성”에 대한 추구는 실제 뇌에서도 발견된다고 한다. 실제 배우 제니퍼 애니스톤을 인식하는 뉴런이 있다고 한다[2]! 이는 하나의 개념을 안정적으로 인지하는 데에 필요한 활성 세포의 개수가 아주 적다는 희소 표상sparse representation을 의미한다고 한다. 희소 표상과 관련해 발달인지 분야의 결정적 시기Critical Period와 가지치기Pruning도 관련이 깊다. 이러한 에너지 효율성은 인공지능 시스템이 돌아가는 워크스테이션에 비해 적어도 400배 이상 효율적이라고 간주할 수 있다고 한다.

3. 민감한 만큼 둔감해지니 전체가 보인다
첫번째 챕터에서 기본적인 추상화/다양성의 문제를 다루었고, 두번째 챕터에서 통계적인 해법과 우리 뇌의 특성을 확인했다. 세번째 챕터에서는 궁극적으로 해결하고자 하는 Specificity-Invariance Dilemma를 다룬다. 민감하면서도 둔감하도록 개념을 추상화하기 위한 해결책으로 (1)필터링, (2)풀링, (3)국소성이 있다.
먼저 (1)필터링의 경우, 컨볼루션 연산을 통해 특정 패턴을 나타내는 정보를 필터링하여 중요한 정보만 확인하고, 나머지는 무시하게 할 수 있다. 다음으로, (2)풀링 혹은 서브샘플링을 활용해 유의미한 정보만을 압축하여 추출하게 할 수 있다. 마지막으로, (3)앞선 필터링과 풀링 모두에 적용되는 국소성으로 주위 정보 수용 영역Receptive Field의 범위를 직접 설정하여 유의미한 국소적 정보의 범위를 채택할 수 있다. 이러한 국소적 배열 패턴Topographic Map은 실제 뇌에서도 등장한다. 일종의 사전 지식을 구조적으로 함축하는 것으로, 의도적으로 귀납적 편향성Inductive Bias을 주는 것이다. 이를 통해 계산의 시공간적, 에너지적 효율성을 높일 수 있다. 이것의 기원에 대한 이론은 아직 드러나지 않았지만, 진화를 통해 획득한 형질이 아닐까 싶다.
이제 컨볼루션 및 풀링 연산, 비선형 함수을 묶어 빌딩 블록Building Block을 만든 후, 다양한 방식으로 쌓아 아키텍처를 고안한다. 이를 통해 정말 원하는 대로 추상화할 수 있도록 해결한다. 이처럼 상향식으로 부분을 통해 전체를 보았다면, 반대로, 하향식으로 전체를 통해 부분을 확인할 수 있는 Attention이 가능하다. 이를 위해 Self-Attention이라는 기술이 등장했지만, 아직 깔끔한 해결책이 등장하진 않았다고 한다.
우리의 뇌는 이러한 부분과 전체의 모순을 해결하기 위해 상향식 개념 추상화와 하향식 주의집중을 하게 된다. 이를 가능하게 하는 수많은 메커니즘 중, 가장 낮은 층에서 상위 개념을 잡아낼 수 있는 메커니즘이 있다고 한다. 이는 망막 신경이 중심에서 주변으로 갈 수록 밀도가 낮아지는 비선형성을 활용한 것으로, 밀도가 낮아 저차원인 주변부의 정보를 최상부로 귀띰해주어 주의집중을 야기하는 원리이다.
- Brain -> AI:
- 대뇌피질의 계산적 원리가 반영된 CNN이 큰 성공을 거두기까지 20년이 걸림.
- 뇌과학이 도움을 주었으면 더 일찍 가능했을 것.
- AI -> Brain:
- CNN과 두뇌의 기능적 유사성에 주목, 대뇌의 정보처리 과정을 연구해보니 각 층의 개별 뉴런과 유사하게 작동했음. 상부상조.
- Predictive Coding Scheme, Illusion?
| Questions:
- 인공신경망과 두뇌의 기능적Functional 유사성이 있다면, 정보 처리의 관점 뿐만 아니라 내적 경험Introspection의 관점에서도 유사한 현상을 관찰할 수 있을 것이다. 인간의 착시/환각 현상과 인공신경망에서의 현상은 무슨 관계가 있을까?
- 대뇌피질에 표상이 국소적으로 배열된 것을 통해 계산의 시공간적, 에너지적 효율성을 높인다는 것이 과연 유의미한 주장일까? 계산모형과 시뮬레이션을 통해 검증해볼 수 있지 않을까?
4. 지극히 주관적이다, 그래서 더 객관적이다
챕터 1~3까지는 어떻게 세상World에서 관측한 결과를 바탕으로 추상화하여 이해할 수 있는가?라는 질문이었다. 챕터 4는 추상화의 반대인 구체화에 대한 이야기로 데이터의 생성을 주제로 한다. 결정론적이었던 앞선 신경망과 달리, 이제부터는 각 뉴론을 확률변수로 대체한 확률론적 신경망을 다루게 된다.
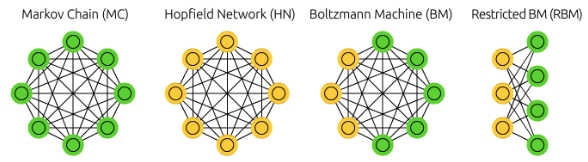
초기 확률론적 신경망으로 홉필드 네트워크Hopfield Network; HN가 있으며, 단순한 통계분석 뿐만 아니라 복잡한 상관관계 분석이 가능하다. 확률론적 신경망은 (1)쉽게 추론이 가능하고, (2)각 요소의 역할을 말해줄 수 있으며, (3)한 요소를 무시하면 잘못된 결론에 도출될 수 있음을 알려줄 뿐만 아니라, (4)꽤 복잡한 상호관계를 찾아낼 수 있다는 장점이 있다.
기존의 홉필드 네트워크에 은닉 뉴런을 추가한 볼츠만 머신Boltzmann Machine; BM은 데이터로부터 가설을 검증할 수 있게 해준다. 이 모형의 목적은 데이터로부터 다양한 인자들 간의 상관관계를 배우는 것이다. 뉴런들 사이를 연결하는 최적의 가중치를 찾아나가는 학습 규칙을 유도하여, (1)데이터 안에서 직접 관찰할 수 있는 인자들 간의 상관성과 (2)네트워크가 현재까지 학습한 상관성 간의 차이를 줄이는 방향으로 이루어진다고 한다. (1)의 경우 데이터를 직접 보면서 계산되는 부분이므로 깨어있는 상태, (2)의 경우 데이터를 보지 않고 네트워크가 추론하는 부분이므로 꿈꾸는 상태로 비유할 수 있어, Wake-Sleep Rule이라고도 불린다.
확률적 신경망이 실제 적용되기 어렵다는 문제를 해결하고자 제한적 볼츠만 머신Restricted Boltzmann Machine; RBM이 등장하게 된다. RBM은 일반 뉴런Visible Neuron과 은닉 뉴런Hidden Neuron 사이의 연결만을 허용하는 방식을 취하여, 은닉 뉴런 사이의 복잡한 상관관계를 사라지게 만든다. 이러한 일반 뉴런층과 은닉 뉴런층의 구조는 하나의 빌딩 블록을 형성하여, 심층 제한적 볼츠만 머신Deep RBM; DRBM이 등장하게 된다. 이때, 오차 역전파 알고리즘을 활용하여 정밀한 학습을 수행하면 결정론적 신경망인 오토인코더Autoencoder;AE가 되게 된다.
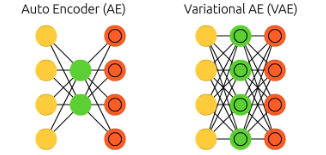
오토인코더와 같이 대칭성을 활용해 개념의 추상화와 구체화를 구현한 것은 주성분분석PCA에서도 확인할 수 있다. 현대에는 대칭성이 깨지더라도 수학적으로 허용되는 선에서 활용되고 있다. 오토인코더의 확률론적 버전으로 변분 오토인코더Variational Autoencoder; VAE가 있으며, (1)오토인코더의 대칭성을 어느정도 유지하면서, (2)추상화 과정에 깊이를 더하고, (3)구체화 과정의 밀도를 높이는 장점을 갖는다고 한다. 마지막으로 재매개변수화Reparametrization 트릭이 적용되어 오차 역전파 알고리즘도 적용될 수 있게 된다.
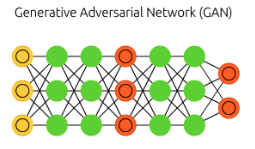
한편, 추상화와 구체화의 성능은 결국 사용자가 정의한 오차함수에 의해 평가되는데, 이러한 자기 평가를 객관화할 수 있도록 하게 위해 게임 이론을 활용하여 생성적 적대적 신경망Generative Adversarial Network; GAN같은 모형이 등장했다. 정보 이론의 관점에서, 기존의 주성분 분석이나 오토 인코더와 같은 결정적 신경망은 KL Divergence를 최소화하는 방식으로 학습된다. 비대칭적인 KL Divergence와 달리, GAN은 대칭적인 JS Divergence를 최소화하게 된다. 이는 경제학의 Optimal Transport 문제로 간주할 수 있고 Wasserstein Distance로 평가할 수 있다.
| Questions:
- 각 확률론적 신경망은 인간의 두뇌와 어떤 관련이 있는가? 뉴런이 확률변수라고 가정하는 것은 실제 뉴런의 랜덤성 때문인가, 아니면 단순한 우리의 가정일 뿐인가?
- 최근 등장하는 StableDiffusion과 같은 Diffusion 기반 생성 모형들은 앞서 설명한 모형들과 어떤 관련성이 있는가?
- 통계역학의 Ising Model, Cellular Automata와 어떤 관련성이 있는가?
5. 과거를 예측하고 미래를 회상하다
챕터 1~3까지 개념의 추상화, 챕터 4에서는 개념의 구체화에 대해 다루었다. 이제는 개념의 시간 여행; 기억에 대해 다룬다. 이전까지는 데이터의 i.i.d 조건을 가정하게 된다. 그러나, 현실은 대부분 독립 사건이 아니다. 때문에, 과거에 생성한 개념을 잊지 않고 기억하는 것이 중요해진다. 이를 구현하기 위한 전략으로 되먹임Feedback이 있다. 실제 대뇌피질, 해마 등에서 가장 많이 발견되는 뉴론 중 하나인 피라미드 뉴런Pyramidal Neuron은 근처 뉴런으로부터 입력을 받을 뿐만 아니라, 이미 정보를 전달한 꽤 멀리 있는 뉴런으로부터 입력을 거꾸로 받기도 한다! 되먹임 신경망Recurrent Neural Network; RNN에서 오차 역전파 알고리즘을 적용하기엔 역전파 발산Exploding Gradient 혹은 역전파 소멸Vanishing Gradient같은 현상이 발생하여 학습이 잘 되지 않는다. 이러한 문제를 해결하고자 장기 기억과 단기 기억을 결합한 장단기 메모리Long-Short Term Memory; LSTM이 있다.
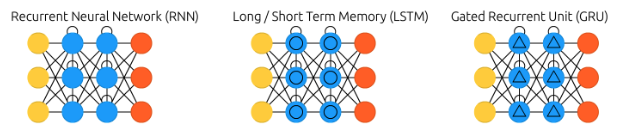
새로운 정보를 유연하게 받아들이면서 오랫동안 안정적으로 기억을 유지할 수 있는 이상적인 신경망은 (1)상황에 적응할 수 있을 뿐만 아니라, (2)새로운 지식을 확장할 수도 있다. 이러한 의미에서 연속 학습Continual Learning 혹은 평생 학습Lifelong Learning이라고 불린다. 더욱이 다양한 작업이나 목표에도 적응할 수 있다는 점에서 다중 도메인 적응Multi-Domain Adaptation, 혹은 다중 작업 학습Multi-Task Learning에도 사용될 수 있다.
인공 신경망은 유동적인 기억 능력이 부족하여, 새로운 정보를 쫓느라 과거의 학습 정보가 증발되는 치명적 망각 현상Catastrophic Forgetting 현상이 발생한다. 이를 해결하기 위해 (1)정규화 기법, (2)과거 데이터 활용, (3)파라미터 활용 등을 적용할 수 있다. 그러나, 최근 자기 주의집중Self-Attention을 활용한 트랜스포머Transformer 모델을 통해, 시공간의 개념을 분리하지 않아, 관찰한 사건들의 과거와 미래의 구분을 없애는 전략을 취한다. 저자의 말을 빌리자면, “과거를 예측하고, 미래를 회상한다”는 것이다!
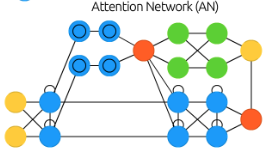
트랜스포머는 앞서 4장에서 다룬 기억의 구체화 문제에서도 효과적으로 작동한다. 시간 순서에 따른 사건들을 종합적으로 이해하는 추상화 과정과 달리, 구체화 과정에서는 순서에 맞게 사건을 재구성할 수 있어야 한다. 이 때 기억의 구체화 신경망은 주Q어진 상황에 맞게 재해석해서 사건을 순서대로 재구성하는 것을 목표로 한다. 이때 주의집중 마스킹 전략Attention Masking을 통해 현재까지의 입력만을 받도록 하여 BERT, GPT같은 좋은 성능을 달성할 수 있도록 하였다.
| Questions:
- 우리의 두뇌는 어떻게 Catastrophic Forgetting 문제를 해결하고 있는가?
- Transformer 모델이 정말 AE와 Attention 기능을 적절히 활용하고 있는가? (World Model의 경우, VAE+RNN+Controller로 구성되어 있다.)
- Transformer 모델의 계산 및 학습 효율성은 어떻게 되는가? 일반 GPU에서 적절히 사용 가능한가?
- Transformer 모델이 Neuroscience의 관점에서 효율적인가?
6. 생각이 시간과 공간을 넘나드는 마법을 부리다
챕터 1~3까지 개념의 추상화, 챕터 4에서는 개념의 구체화, 챕터 5에서는 기억에 대해 다루었다. 이제는 신경망의 학습 원리에 대해 다루고자 한다. 현재 신경망의 가중치 전달 과정Weight Transport에 사용되는 오차 역전파 알고리즘은 벨만의 동적 계획법을 활용한다. 일종의 "전지적 작가 시점God Mode"인 것이다. 정말 우리의 뇌도 이런 식으로 작동할까?
딥마인드의 연구 결과에 따르면, 심지어 가중치 정보를 제거한 후 난수를 학습시키는 역전파 정렬Feedback Alignment만으로도 학습이 가능했다! 적어도 생물학적 신경망은 전지적 작가 시점의 오차 역전파 알고리즘 대로 학습하지 않는 셈이다.
하나의 뉴런이 지니는 신경 가소성Synaptic Plasticity은 (1)장기 강화Long-Term Potentiation과 (2)장기 억압Long-Term Depression의 전체적인 변화 과정으로 구성된다. 이 두 과정은 뉴런들의 수상돌기가 지닌 동적 반응 특성(수상돌기의 민감도 변화)으로 일어나는 상대적인 타이밍 차이로 야기된다는 점을 고려하면, 생물학적 신경망은 전지적 작가 시점이 아닌 "1인칭 주인공 시점First-Person Mode"인 것이다.
연구자들은 신경 가소성을 인공 신경망에 담기 위해 시간적 오차 모델Temporal Error Model, 이후 예측 코딩 모델Predictive Coding Model을 개발했다. 예측 코딩 모델은 오류 노드를 포함하여 뉴런의 전달의 정확도를 평가한다.
한편, 수상돌기는 일종의 정규화 연산을 수행한다. 수상돌기의 크기가 큰 신경세포는 다양한 입력 채널의 입력값에 둔감하게 반응하게 되어 둔감성을 유지한다. 다시말해, 정보량의 차이가 커지더라도 안정적으로 작동한다는 것이다. 이때, 국소적인 연결이 많은 수상돌기는 기저수상돌기Basal Dendrite, 전역적인 연결이 많은 수상돌기는 선단수상돌기Apical Dendrite라고 부른다. 최근 연구에 따르면 기저수상돌기는 적어도 얕은 인공 신경망, 선단수상돌기는 하나 이상의 은닉층을 가진 신경망과 비슷한 연산 능력을 지니고 있다고 한다.
| Questions:
- 신경 가소성의 동적 특성을 바탕으로 한 학습 알고리즘이 있는가?
- 물리적인 관점에서 흥미롭게 본 Critical Brain Hypothesis의 경우, 역전파 정렬 현상을 설명할 수 있을까?
- 뉴런이 하나의 랜덤 변수라고 생각하면, 노이즈의 중요성은 무엇일까?
- 예측 코딩보다 Active Inference가 더 좋은 설명을 제공해 줄 수 있을 것인가?
7. 미래를 내다보며 과거를 바꾼다
챕터 1~3까지 개념의 추상화, 챕터 4에서는 개념의 구체화, 챕터 5에서는 기억, 챕터 6에서는 신경망의 학습 원리를 다루었다. 마지막 7장에서는 강화학습을 다루고자 한다. 강화학습은 기본적으로 동적 시스템의 전략 또는 정책을 학습하는 문제로 귀결된다. 다만, 전략이 실제로 수행될 때, 과거 전략이 현재의 경험에 얼마나 기여했는지에 대한 시간적 기여도 할당 문제Temporal Credit Assignment를 해결할 필요가 있다.
벨만의 동적 계획법Dynamic Programming과 최적성의 원리Principle of Optimality는 이러한 문제를 해결해주는 방법 중 하나로, 복잡한 문제를 쉬운 문제를 재귀적으로 풀어나가며 해결한다. 보다 구체적으로, Markov Decision Process라는 수학적 형식 위에서 벨만 방정석을 정의할 수 있고 주어진 환경으로부터 얻은 보상예측오류를 활용해 강화학습을 수행할 수 있다.
알파고와 같은 강화학습 알고리즘은 모델 프리 강화학습Model-Free Reinforcement Learning;MFRL을 활용하여 문제를 해결한다. 그러나 이러한 알파고의 습관적 행동을 분석해보면, 결과에 집착하는 행동Devaluation Insensitivity를 관찰할 수 있다. MFRL은 목적이 유연하게 변해야 하는 경우, 기민하게 행동하지 못한다는 단점을 갖고 있다. 실제로, 동물들의 행동을 관찰하면 대개 결과지향적 태도를 확인할 수 있다. 1977년 연구 결과(울프람 슐츠, 피터 다이안, 리드 몽타규)에 따르면, 원숭이의 중뇌 부위의 도파민 신경세포 활성도가 변화하는 모습이 모델 프리 학습 알고리즘의 보상 예측 오류 신호와 닮았다는 것을 밝힌다. 2004년에는 인간 중뇌의 선조체Striatum가 MFRL의 중추임을 발견했다!
이러한 단점을 해결할 수 있도록, 목표지향적 행동을 구현해내는 학습 방식을 모델 기반 강화학습Model-Based Reinforcement Learning;MBRL이 제안되어 왔다. 이 모델은 목표와 원리를 분리하여 다양한 상황의 다양한 목표를 달성할 수 있도록 설계되었다. 물론, 문제가 너무 복잡하거나 환경의 불확실성이 높아 모델을 학습하기 어려운 경우 잘 작동하지 않는다는 단점을 갖고 있다. MFRL과 유사하게, MBRL도 과학적 역사가 깊다. 1930년대 연구 결과(에드워드 톨만), 쥐 실험을 통해 보상이 없는 상황에서도 잠재학습Latent Learning이 발생하고 이를 통해 환경에 대한 정보인 인지맵Cognitive Map을 형성한다는 것을 밝힌다. 예상하는 상황과 현실 상황의 괴리로부터 상태 예측 오류를 통해 학습하는 것이다! 이후 쥐의 경우, 변역계Limbic System을 중심으로 변연계 아래피질Infralimbic Cortex, 인간의 경우, 측전전두피질Lateral Prefrontal Cortex와 두정엽내고랑Intraparietal Sulcus 등에서 MBRL의 중추임을 발견했다.
한편, 최적 제어 이론의 모델 예측 제어Model Predictive Control의 경우가 모델 기반의 방법론을 활용하며, 모델 기반 학습의 시초라고 평가되기도 한다. 행동심리경제학에서는 MFRL과 같이 반자동적이고 빠른 의사결정 방식을 “시스템 1”, MBRL과 같이 의식적이고 느린 의사결정 방식을 “시스템 2“라고 부른다.
2005년 런던 대학의 연구팀은 더욱 과감한 질문을 던지는데, 동물의 뇌가 결과를 얘측할 때의 불확실성에 따라 MFRL과 MBRL을 스위칭한다는 것이다. 실제로 2015년, 인간의 측전전두피질과 전두극피질Frontopolar Cortex에서 이러한 불확실성 정보를 처리하고 있고, 이를 바탕으로 두 전략을 조합하는 방식으로 학습 과정을 제어하고 있음을 밝혔다! 다시 말해, 주어진 ‘사건Event’에서 ‘상황Context’을 읽어내고, 그 속에서 ‘문제Task’에 초점을 맞추게 되는 메타 인지가 작동하는 셈이다.
| Questions:
- MBRL과 MFRL의 장단점에 대해서 잘 찾아보자.
- 두 패러다임과 대니얼 카너먼의 시스템 I vs II가 정말로 매칭되는 개념인가?
- 메타 인지는 고차 사고를 의미하는가? MBRL과 MFRL의 스위칭 원리는 단순한 2차적 사고에 불과한가?
- Active Inference는 더욱 큰 설명력과 이론을 제공할 수 있겠는가?
Reference
[1] 인공지능과 뇌는 어떻게 생각하는가, 출판사 ‘솔’, 이상완 지음, 2022
[2] 얼굴 인식하는 신경세포 따로 있다, The Science Times, 심재율 객원기자, 2019 2/12,
[3] Van Veen, F., & Leijnen, S. (2019). The Neural Network Zoo. The Asimov Institute. https://www.asimovinstitute.org/neural-network-zoo/


Comments