빠르고 안정적인 자율주행 기술을 향하여
“우리가 살아가는 세상은 복잡하고(Complex), 비선형적이며(Noninear), 불확실하다(Uncertain). 우리는 어떻게 이렇게 혼란스러운 세상 속에서 궁극적인 전략을 생성하여 영속할 수 있는 걸까? 우리는 로봇들로 하여금 그러한 전략을 스스로 학습하고 발견하게 할 수 있을까?”
차량, 로봇, 원전 등 다양한 기계 장치에 대해 생각해보자. 그들은 모두 센서, 볼트와 너트, 모터 등의 작은 기계 장치들로 구성된 시스템(System)이다. 우리는 이러한 시스템이 우리가 원하는 대로 적절한 행동을 수행하길 바란다. 운전(Driving)의 문제를 생각해보자. 우리는 매일 아침과 저녁, 우리 눈과 귀를 활용해 먼 곳에서 가까운 곳까지 지각하여, 오른 발의 페달을 적절히 제어하며 운전해 나간다. 이러한 행동을 모사해내는 기계장치 혹은 소프트웨어를 구현하려면 어떻게 해야 할까?
본 글은 자율 주행(Autonomous Driving) 분야와 관련된 최적 제어 이론(Optimal Control Theory)을 공부하며 깨달은 부분들을 쉽고 간결하게 정리하는 것을 목표로 한다. 특히, 최근 강화학습과 더불어 각광받는 모델 기반 예측 제어(Model Predictive Control, 이하 MPC)에서 유명한 정보 이론 기반의 MPC(Information-Theoretic MPC) 알고리즘을 다루려고 한다.
1. 최적 제어 이론의 창시
주어진 시스템을 최적의 방식으로 제어하려는 시도는 과거 사이버네틱스 운동에서 깊게 다뤄졌으며, 이후 최적 제어 이론(Optimal Control Theory; 이하 OCT)으로 발전하게 되었다. 이 분야는 기계 장치로 하여금, 그들이 취할 수 있는 행동 중 우리가 원하는 최적의 행동을 하게 하기 위한 이론적 프레임워크와 공학적 설계 방법론을 제공해준다. 최적 제어 이론은 강력한 수학적 배경지식을 요구한다. 왜냐하면, 이 분야는 서로 다른 두 명의 천재 수학자; 미국의 리처드 벨만(Richard E. Bellman)과 구 소비에트 연방의 레프 폰트랴긴(Лев Семёно́вич Понтря́гин)에 의해 창시되었기 때문이다.
1.1 리처드 벨만과 레프 폰트랴긴


먼저, 자신의 자서전 “태풍의 눈(Eye of the Hurricane)“으로도 유명한 벨만은 과거 1950년대 RAND(Research and Development) 연구소에서 미사일의 제어와 관련된 문제를 다루게 된다. 벨만은 컴퓨터 공학과의 알고리즘 수업에서 반드시 배우는 동적 프로그래밍(Dynamic Programming)의 발명자이다. 동적 프로그래밍이란 문제의 재귀성(Recursivity)을 활용해 반복적인(Iterative) 계산과 메모리 할당으로 복잡한 문제를 쉽게 푸는 방법이다. 그는 자신의 알고리즘을 과거 19세기 물리학자/수학자 해밀턴(William Rowan Hamilton)과 자코비(Carl Gustav Jacob Jacobi)가 입자의 움직임을 파동으로 표현한 해밀턴-자코비 방정식(Hamilton-Jacobi Equation)에 적용한다. 이를 후대에는 해밀턴-자코비-벨만 방정식(Hamilton-Jacobi-Bellman Equation)이라고 부르며, 줄여서 HJB 방정식이라고 부른다.
한편, 폰트랴긴은 눈이 보이지 않는 시각 장애를 가졌음에도 다양한 분야에서 괄목할 만한 업적을 남긴 것으로 유명하다. 그는 폰트랴긴 최소 원리(Pontryagin’s maximum principle)를 통해 벨만의 HJB 방정식 유도와 유사한 결론을 얻었다. 그는 보다 엄밀하고 풍부한 수학을 사용했는데, 그의 이론은 추후 노벨 경제학상을 수상한 칸토로비치에 의해 경제학에 적용되었다.
폰트랴긴의 접근법은 수학적으로 상미분 방정식을 활용했으며, 그의 접근은 해밀토니안 방정식과 유사하다는 특징이 있다. 다만, 경계 조건에 의존적이라 실제로 푸는 데 어려움이 있었다. 한편, 벨만의 접근법은 편미분 방정식을 활용하여, 이후 추가적인 잡음(noise) 항을 추가하기 용이했다. 물론, 차원의 저주로 인해 문제를 풀어내는 데에는 문제가 있었다.
1.2 이산 시간 최적 제어 문제
최적 제어 문제(Optimal Control Problem)은 총 세 가지 개념으로 구성된다. 먼저, 시간, 공간, 제어 변수에 의해 변화하는 동역학계가 주어져야 한다. 먼저 이산 시간에 따른 동역학계를 고려하자. 시간 변수를 $t$, 시스템의 변수를 $x_t$, 제어 변수를 $u_t$라고 하자. 그러면 아래 수식에서 $f$가 바로 동역학계를 의미한다:
\[x_{t+1} = f(t, x_t, u_t), \ \ t= 0,1,...,T \cdots (1)\]이 동역학계는 특정 시간, 상태와 제어에 따라 보상(벨만) 또는 비용(폰트랴긴) $R(t,x_t,u_t)$이 있으며, 이를 활용해 주어진 시간 동안의 누적 비용 $C(x_0,u_{0:T})$을 말할 수 있게 된다. 이때 누적 비용 $C(x_0,u_{0:T})$가 초기 시스템 상태 $x_0$와 제어 입력들 $u_{0:T}$에만 의존하는 이유는 두 가지 정도로 표현할 수 있겠다. 첫번째 이유는 초기값과 이후 입력만 주어지면 동역학계 $f$를 통해 전체 시스템의 궤적을 계산할 수 있기 때문이다. 두번째는, 실무적 관점에서 각 시점의 시스템 상태는 센서를 통해 추론되는 경우가 많으므로 초기값 외에는 모른다고 가정하는 것이 합리적이기 때문이다:
\[C(x_0, u_{0:T}) = \sum_{t=0}^{T} R(t,x_t,u_t) \cdots (2)\]이제 최소 비용을 주는 최적 입력에 대해 말할 수 있다. 최적 입력(Optimal Control) $J(t, x_t)$는 현재 시점 $t$를 기준으로 앞으로 특정 시간 $T$까지의 비용을 최소로 만들어주는 입력이다. 즉:
\[J(t, x_t) = \min_{u_{t:T}} \sum_{s=t}^{T} R(s,x_s,u_s) \cdots (3)\]이때, 최적 입력은 재귀 관계(Recursive Relation)을 갖는다. 이는 아래의 수식 전개를 통해 잘 드러나며, $J(t,x_t)$는 $J(t+1,x_{t+1})$로부터 계산될 수 있음을 보여준다:
\[\begin{align} \underline{J(t,x_t)} & = \min_{u_{t:T}} \sum_{s=t}^{T} R(s,x_s,u_s) \ by\ definition \\ & = \min_{u_t}\left( R(t,x_t,u_t) + \min_{u_{t+1:T}} \sum_{s=t+1}^{T} R(s,x_s,u_s) \right) \\ & =\min_{u_t}\left( R(t,x_t,u_t) + J(t+1, x_{t+1}) \right) \\ & =\min_{u_t}\left( R(t,x_t,u_t) + \underline{J(t+1, f(t,x_t,u_t))} \right) \cdots (4) \end{align}\]위 관계식으로부터 벨만의 동적 프로그래밍을 적용하면 원하는 시점 $T$ 이후부터는 $J(T+1,x)=0$으로 초기화한 후, 역으로 계산해 최적 입력을 계산해 나갈 수 있다.
1.3 연속 시간 최적 제어 문제
이산 시간에서의 최적 문제와 관련된 수식 (1), (2), (3), (4)와 마찬가지로, 연속 시간 $t$에 따른 실변수 $x, u$에 대해 생각해볼 수 있다. 먼저, 문제의 구성요소는 다음과 같이 표현할 수 있다. 이때, $\phi(x(t_f))$는 최종 시스템 상태에 대한 특수 비용을 의미한다:
\[\begin{align} \dot{x} & = f(x,u,t) \cdots (5)\\ C(t_i, x_i, u(t_i \rightarrow t_f)) & = \phi(x(t_f)) + \int_{t_i}^{t_f} dt R(x(t),u(t),t) \cdots (6)\\ J(t,x) & = \min_{u(t_i \rightarrow t_f)} C(t,x,u(t \rightarrow t_f)) \cdots (7)\\ \end{align}\]그러면, 최적 입력 $J(t,x)$는 수식 (4)와 같이 다음과 같은 재귀 관계를 지니게 된다(수식 전개 과정은 생략한다):
\[\underline{J(t,x)} = \min_{u(t \rightarrow t')} \left( \int_{t}^{t'} dt R(x(t),u(t),t) + \underline{J(t', x(t'))} \right) \cdots (8)\]이때, $t’$가 $t$와 아주 작은 시간 간격 이후라고 가정하면; 즉, $t’ = t + dt$을 대입하고 $dt \rightarrow 0$의 극한을 취하면 다음과 같은 편미분 방정식을 얻을 수 있다. 이 방정식이 바로 HJB 방정식이다.
\[\begin{align} - J_t(t,x) & = \min_{u} \left( R(x,u,t) + J_x(t,x)f(x,u,t) \right) \\ J(x,t_f) & = \phi(x) \end{align} \cdots (9)\]2. 확률적 최적 제어 이론으로의 발전

기존의 최적 제어 이론은 훌륭한 이론적 프레임워크를 제안하는 데에는 성공했으나, 컴퓨터를 활용해 해답을 구하는 과정이 너무나 오래 걸렸다. 이에 더해, 동역학계 모델 $f$를 역으로 추정하거나 변수 $x$의 참값을 측정하거나 정확한 입력 $u$를 적용하는 데에도 한계가 있었다. 그러던 와중, 네덜란드의 물리학자 힐버트 카펜(Hilbert J. Kappen)은 HJB 방정식에 잡음 항(Noise Term)을 추가함으로써 이를 해결하기 시작했다. 그는 네덜란드의 랏바우트 대학교(Radboud University)의 생물물리학과에 속한 물리학 교수로, 기계 학습의 물리적 과정(The Physics of Machine Learning)에 초점을 맞추어 연구를 수행하고 있다. 그렇다면 여기서 그가 추가한 잡음(Noise)란 무엇인가?
2.1 위너 프로세스


수학에서 위너 과정(Wiener Process)은 미국의 수학자이자 사이버네틱스 운동의 창시자인 노버트 위너(Norbert Wiener)에 의해 발견된 연속 시간 확률 과정(Continuous-Time Stochastic Process)이다. 이는 종종 아인슈타인이 연구했던 물 속 꽃가루의 움직임을 다루는 브라운 운동(Brownian Motion)으로도 표현되는데, 형식적으로는 깊은 관계를 갖는다. 대부분의 자연 현상은 잡음이 포함되어 있으며, 수많은 확률 과정에서도 또한 공통적으로 발견할 수 있다. 기존의 최적 제어 이론은 결정론적인(Deterministic) 가정을 도입하여 확률의 개입을 막았지만, 수많은 실제 문제에서는 확률 과정의 도입이 필요해 보인다. 이 위너 과정이야 말로 수학적으로, 물리적으로 자연스러운 잡음으로 생각하면 된다.
위너 과정의 수학적 정의를 파악해보자. 어떤 확률 과정 $W_t$가 다음의 특징을 만족하면 위너 확률 과정이라고 부른다:
- $W_0 = 0$.
- 임의의 $t>0$에 대해, 미래의 변화량 $W_{t+u} - W_t, u \leq 0$은 과거의 값들 $s < t$인 $W_s$에 대해 독립이다.
- $W_{t+u} - W_t \sim \mathit{N}(0, \nu)$.
- $W_t$는 $t$에 대해 연속이다.
미적분과 관련해, 위너 확률 과정의 시간에 대한 변화량 $d\xi$는 다음과 같은 성질을 지닌다. 이 특징은 아인슈타인이 발견한 결론과도 유사하다. 아인슈타인은 브라운 운동에 대한 공식에서, 거리 제곱의 평균이 시간에 비례한다는 결론을 내렸다. 이 결론은 아래의 성질과 일맥상통한다:
\[<d\xi^2> = \nu dt \cdots (10)\]2.2 확률적 최적 제어 문제
앞서 연속 시간 최적 제어 문제의 수식 (5), (6), (7), (8)에 대해 위너 과정 기반의 잡음 항을 추가할 수 있다. 이렇게 추가된 확률적 최적 제어 문제는 다음과 같이 기술할 수 있다. 수식 (13)에서 또한 재귀 관계를 확인할 수 있다:
\[\begin{align} dx & = f(x(t),u(t),t)dt + d\xi \cdots (11)\\ C(t_i, x_i, u(t_i \rightarrow t_f)) & = \biggl< \phi(x(t_f)) + \int_{t_i}^{t_f} dt R(x(t),u(t),t) \biggr>_{x_i} \cdots (12)\\ \underline{J(t,x)} & = \min_{u(t_i \rightarrow t_f)} \biggl< \int_{t}^{t'} dt R(x(t),u(t),t) + \underline{J(t', x(t'))} \biggr>_{x} \cdots (13)\\ \end{align}\]이때, $t’$가 $t$와 아주 작은 시간 간격 이후라고 가정하면; 즉, $t’ = t + dt$을 대입하고 $dt \rightarrow 0$의 극한을 취하면 다음과 같은 편미분 방정식을 얻을 수 있다. 특히 아래 식을 얻는 과정에서 수식 (10)을 적용하여 확률변수의 증분 제곱의 평균 $<d\xi^2>$을 해당 위너 프로세스의 분산 $\nu dt$로 대체할 수 있다. 이렇게 얻은 아래의 방정식이 바로 확률적 해밀턴-자코비-벨만 방정식(Stochastic Hamilton-Jacobi-Bellman Equation; sHJB)이다.
\[\begin{align} - \partial_{t} J(t,x) & = \min_{u} \left( R(x,u,t) + f(x,u,t)^{T} \partial_{x} J(t,x) + \frac{1}{2}\nu \partial_{x}^2J(t,x) \right) \\ J(x,t_f) & = \phi(x) \end{align} \cdots (14)\]3. 경로 적분 프레임워크
이렇게 구한 sHJB 방정식은 비선형 편미분 방정식이기 때문에 일반해를 구하기 무척 어렵다. 카펜은 근사 해(Approximation Solution)에 대한 시뮬레이션 결과를 얻을 수 있도록 경로 적분의 꼴로 변환하는 전략을 취한다. 일단 이 방정식을 경로 적분 형태로 변형시키려면, 몇가지 가정이 필요하다.
3.1 LQ 문제로 축소
sHJB 문제를 선형화하려면 먼저 몇가지 가정을 도입해 문제를 축소할 수 있다. 먼저, 동역학계에 대한 제어 입력의 선형화(Linearization)이다. 두번째는 비용에 대한 제어 입력의 이차화(Quadratization)이다. 이 두 가정이 적용된 문제를 LQ 문제라고 표현한다.
쉽게 표현해보면, 앞서 정의한 확률적 최적 제어 문제를 다시 생각해보자. 수식 (11)에서 동역학계가 제어 입력에 대해 선형적 관계를 유지한다는 것은 동역학계 $f$를 (1)제어에 독립적인 부분과 (2)제어 입력에 선형적으로 의존하는 부분으로 분리할 수 있음을 의미한다. 즉:
\[f(x,u,t) = b(x,t) + Bu\]마찬가지로, 제어 입력이 비용에 대해 이차항의 관계를 지닌다는 것은, 수식 (12)에서 보상 항 $R(x,u,t)$를 (1)제어에 독립적인 부분과 (2)제어 입력에 이차적으로 의존하는 부분으로 분리할 수 있음을 의미한다. 즉:
\[R(x,u,t) = V(x,t) + \frac{1}{2} u^T R u\]따라서 이 가정을 적용하여 확률적 최적 제어 문제를 축소해보면, 다음과 같이 정리할 수 있다.
\[\begin{align} dx & = \left( b(x,t) + Bu \right)dt + d\xi \cdots (15) \\ C(t_i, x_i, u(t_i \rightarrow t_f)) & = \biggl< \phi(x(t_f)) + \int_{t_i}^{t_f} dt \left( V(x(t),t) + \frac{1}{2} u(t)^T R u(t) \right) \biggr>_{x_i} \cdots (16) \\ \end{align}\]이를 적용해 유사한 방식으로 sHJB 방정식을 유도하면, 다음과 같은 축소된 방정식을 얻을 수 있다:
\[\begin{align} - \partial_{t} J & = \min_{u} \left( V + \frac{1}{2} u^T R u + (b + Bu)^{T} \partial_{x} J + \frac{1}{2} \mathrm{Tr} \left( \nu \partial_{x}^2J \right) \right) \\ J(x,t_f) & = \phi(x) \end{align} \cdots (17)\]롤의 정리(Rolle’s Theorem)에 의해 우변이 0이 되도록 만드는 $u$를 찾아 정리하면. 다음과 같이 표현할 수 있다(찾는 과정은 생략한다).
\[u=-R^{-1}B^T \partial_{x} J(x,t)\]이 최적해의 후보를 수식 (17)의 우변에 대입하면, 다음과 같이 정리할 수 있다.
\[\underline{- \frac{1}{2} (\partial_{x} J)^T BR^{-1}B^T (\partial_{x} J)} + V + b^{T} \partial_{x} J + \underline{\frac{1}{2} \mathrm{Tr} \left( \nu \partial_{x}^2J \right)} \cdots (18)\]3.2 Log 변환
보다 시피, sHJB 방정식 LQ 가정으로 축소했더라도 $J$에 대한 이계 미분 항이 남아 있어 아직은 비선형 방정식이다(수식 (18)의 밑줄 친 항을 보라). 이때 이 방정식을 선형화할 수 있도록 로그 변환을 통해 수식을 선형화해보자. 즉 기존의 $J$ 대신 새로운 $\psi$를 도입하는 것이다. 이때 비례 상수는 미래의 수식 전개를 고려하여 $-\lambda$로 설정한다. 즉:
\[J(x,t) = - \lambda \log \psi(x,t) \cdots (19)\]이를 수식 (18)의 밑줄 친 이차항에 적용하면, 다음과 같이 수식을 변형할 수 있다.
\[\begin{align} - \frac{1}{2} (\partial_{x} J)^T BR^{-1}B^T (\partial_{x} J) + \frac{1}{2} \mathrm{Tr} \left( \nu \partial_{x}^2J \right) & = \underline{- \frac{\lambda^2}{2 \psi^2} \sum_{i, j} (\partial_x \psi)_i (BR^{-1}B^T)_{i,j}(\partial_x \psi)_j}\\ & \quad +\underline{\frac{\lambda^2}{2 \psi^2} \sum_{i, j} \nu_{i,j} (\partial_x \psi)_i (\partial_x \psi)_j} \\ & \quad -\frac{\lambda}{2 \psi} \sum_{i,j} \nu_{i,j} \frac{\partial^2 \psi}{\partial x_i \partial x_j}. \end{align}\]이 식이 일차식이 되려면 밑줄 친 첫번째와 두번째 항의 합이 0이 되어야 한다. 그에 따른 필요 충분 조건은 적절한 비례 상수 $\lambda$의 존재성으로 해석할 수 있다. 즉, 우리가 어떤 비례 상수를 갖는 로그 변환을 할 지 결정하면 된다는 것이다. 그 적절함의 기준을 형식적으로 유도해 작성해내면 다음과 같다.
\[\exists \ a\ scalar\ \lambda \mid \nu = \lambda B R^{-1} B^T \cdots (20)\]3.3 Kolmogorov 역향 방정식
만약 수식 (20)을 만족하는 적절한 비례상수 $\lambda$를 선택하여 로그 변환을 취했다고 가정하자. 그러면 수식 (18)은 선형 방정식으로 전체적인 기존의 sHJB 방정식은 아래와 같은 형태가 된다. 아래의 형태는 과거 소비에트 연방의 수학자 안드레이 콜모고로프가 개발한 편미분 방정식으로, 콜모고로프 역향 방정식(Kolmogorov Backward Equation)이라고도 불린다. 일반적으로 이 방정식은 연속 시간, 연속 상태의 마코프 과정에 대한 연구에서 파생되었다. 시스템의 현재 상태에 대한 정보(확률 분포)로부터 미래 상태에 대한 정보(확률 분포)를 파악할 때 유용하다.
\[\begin{align} - \partial_t \psi & = H\psi,\ where\ an\ operator\ H = \left( \frac{V}{\lambda} + b^T\nabla + \frac{1}{2} \nu \nabla^2 \right) \end{align} \cdots (21)\]한편, 미국의 이론 물리학자인 리처드 파인만과 수학자인 마크 칵은 원자 폭탄과 관련된 맨해튼 프로젝트에서 중성자의 무작위적 궤적을 계산하기 위해 파인만-칵 공식(Feynman-Kac Formula)을 개발하였다. 이 공식을 활용하면 확률 과정에 따른 무작위적인 궤적을 시뮬레이션함으로써, 수식 (21)과 같은 편미분 방정식을 풀 수 있게 만들어준다. 공식에 대해 자세히 다루진 않겠지만, 이를 적용하면 다음과 같이 수식을 전개할 수 있다:
\[J(x,t) = -\lambda \log \int [dx]_x \exp{ - \frac{1}{\lambda} S(x(t \rightarrow t_f))} + C \cdots (22)\]이 때, 수식 (22)에서 등장하는 $S$는 (1)최종 시스템 상태에 대한 제약 조건과 (2)시스템의 시간에 따른 궤적의 비용으로 해석할 수 있으며, 구체적 수식은 다음과 같다:
\[\begin{align} S(x(t \rightarrow t_f)) & := \phi(x(t_f)) + \underline{S_{path}(x(t \rightarrow t_f))} \\ & = \phi(x(t_f)) + \underline{\int_{t}^{t_f} d\tau \left( \frac{1}{2} \left( \frac{dx(\tau)}{d\tau} - b(x(\tau), \tau) \right)^T R \left( \frac{dx(\tau)}{d\tau} - b(x(\tau), \tau) \right) + V(x(\tau), \tau) \right)} \end{align} \cdots (23)\]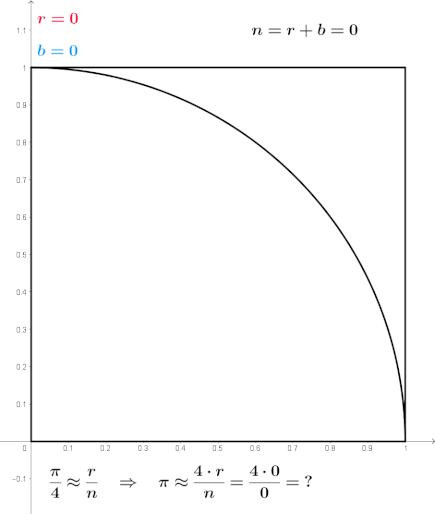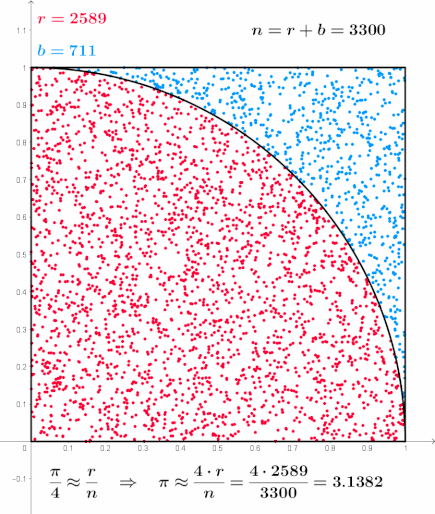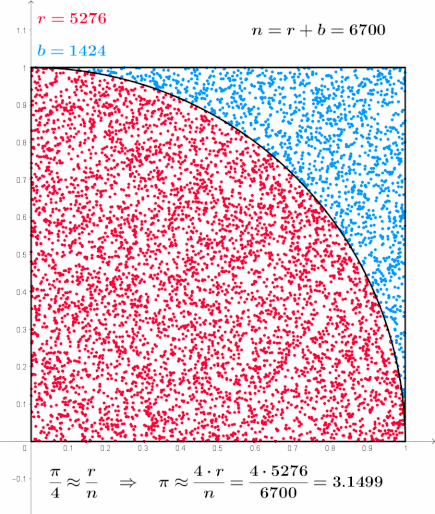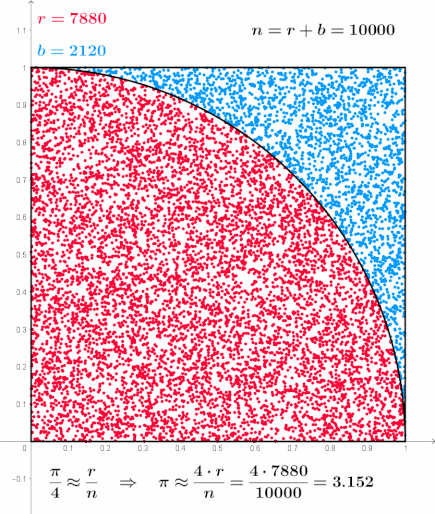
위 경로 적분의 형태는 통계학의 샘플링(Sampling) 기법을 활용해 계산할 수 있다. 카펜은 그의 논문에서 간단한 마코프 체인 샘플링(MC Sampling) 기법을 통해 시뮬레이션을 수행한다.
3.4 열역학 및 강화학습과의 관계
수식 (22)는 사실 정보 이론에서 자주 등장하는 자유 에너지(Free Energy)의 형태와 아주 유사하다. 수식에 등장하는 log 안의 적분 꼴은 통계 역학에서 등장하는 분배 함수(Partition Function)이다. 전체적으로는 분배 함수에 로그가 취해진 꼴로, 자유 에너지로 해석할 수 있다.

또한, 최근 각광 받는 강화학습(Reinforcement Learning )과도 관련성을 지니고 있다. 강화학습은 정상(Stationary) 상태의 환경에서 할인된 미래 보상(Discounted future reward)에 대해 최적 제어 문제라고 볼 수 있다. 다만, 최적 제어 이론은 유한한 미래 상황을 고려하는 반면, 강화학습은 무한한 미래를 다루는 경향이 있다. 또 제어 입력과 비용에 대한 용어도 다른데, 강화학습은 최적 정책(Policy)과 가치(Value)라는 개념을 사용한다. 최적 제어 이론은 효과적인 제어기(Controller)를 개발하고자 하는 반면, 강화학습은 에이전트(Agent)를 개발하는 것을 목표로 한다.
4. 정보 이론 프레임워크

힐버트 카펜은 경로 적분 프레임워크를 개발하여, 최적 제어를 구하는 최적화 문제에 대한 효과적 방법론을 제안했다. 그의 시도는 고전적인 최적 제어 이론에서 시작해, 현대적인 과학적 계산(Scientific Computing)에 맞게 진화했다. 이러한 시도와 정반대로, 조지아 공과 대학교의 에반겔로스 테오도루는 정보이론에서 역 방향으로 접근한다. 그는 정보이론의 변분 자유 에너지로부터 HJB 방정식을 유도해낸다. 이를 이해하려면, 확률과 정보 이론에 대한 기초 지식부터 알 필요가 있다.
4.1 자유 에너지

자유 에너지를 설명하기 전에 먼저, 정보에 대해 소개할 필요가 있다. 정보 이론은 1940년대, 미국의 수학자 클로드 섀넌(Claude Elwood Shannon)이 개발한 이론으로 주어진 (확률) 변수에 대한 불확실성(Uncertatinty)을 표현하기 위해 개발되었다. 그에 따르면 어떤 확률 변수 $X$와 그에 따른 확률 분포 $P_X(X=x)$가 주어지면, 특정 사건에 대한 자기 정보(Self-Information)를 다음과 같이 $- \log$를 취해 표현할 수 있고, 그 형태가 고유하다. 이는 확률이 높은 사건일 수록 불확실성이 줄고, 정보가 많다고 느끼는 직관과도 잘 맞는다. 이때 전체 분포를 바탕으로 각 사건들에 대한 정보의 평균을 취한 것을 엔트로피로 정의한다. 해당 확률 변수가 지닌 평균적인 불확실성인 셈이다.
\[\begin{align} I(X=x) & = - \log P_X(X=x) \cdots self-information\ of\ x \\ \mathcal{E}(X) & = \mathbb{E}_{x \sim P_X} \left[ - \log P_X(X=x) \right] \cdots entropy\ of\ X \end{align}\]이때, 자유에너지는 주어진 임의의 확률 분포 $\mathbb{P}$와 이를 통해 측정 가능한(measurable) 함수 $J$, 0이 아닌 실수 파라미터인 $\rho \in \mathbb{R}^{\neg 0}$에 의해 다음과 같이 정의한다. 즉, 확률 분포 $\mathbb{P}$의 관점에서 측정 가능한(measurable) 함수 $J$의 자유 에너지는 다음과 같다:
\[\mathcal{F} = \log_{e} \int \exp \left( \rho \mathcal{J}(x) \right) \mathbb{d}\mathbb{P} \cdots (24)\]이때, 실제 확률 변수가 따르는 분포 $\mathbb{P}$를 알 수 없으므로, 변분 추론(Variational Inference)의 맥락에서 $\mathbb{Q}$를 도입해보자. 그러면, 두 분포의 차이를 쿨백-라이불러 발산(Kullback-Leibler Divergence)으로 표현할 수 있다:
\[\begin{align} \mathbb{KL(Q||P)} & = \mathbb{E}_{X \sim Q}\left[ \log{\mathbb{Q}(X)} - \log{\mathbb{P}(X)}\right] \\ & = \int \log_{e} \frac{\mathbb{dQ}}{\mathbb{dP}} \mathbb{dQ} \end{align}\]이제 자유 에너지에 쿨백-라이불러 발산을 도입하면, 르장드르 변환(Legendre Transform)에 의해 아래와 같은 부등식을 얻을 수 있다. 이 때 등호 조건은 아래와 같다:
\[\begin{align} - \frac{1}{|\rho|} \log_{e} \mathbb{E_P} \left[ \exp(-|\rho|\mathcal{J}) \right] & \leq \left[ \mathbb{E_Q}(\mathcal{J}) + {|\rho|}^{-1} \mathbb{KL(Q||P)} \right] \\ & = \inf_{\mathbb{dQ}} \left[ \mathbb{E_Q}(\mathcal{J}) + {|\rho|}^{-1} \mathbb{KL(Q||P)} \right],\ when\ \mathbb{dQ^*} = \frac{\exp(- |\rho| \mathcal{J}) \mathbb{dP}}{\int {\exp(- |\rho| \mathcal{J}) \mathbb{dP}} } \end{align} \cdots (25)\]4.2 최적 제어 문제
앞서 소개한 확률적 최적 제어 문제와 경로 적분 프레임워크의 결론을 참고하여 풀고자 하는 문제로 형식화해보자. 먼저, 비용함수 $\mathcal{J}$를 최종 상태 $t_N$에만 의존하는 비용 $\phi(\mathbb{x}(t_N), t_N)$와 특정 시간과 상태에서의 비용 $q(\mathbb{x}, \tau)$를 적분한 궤적의 운영 비용 $\int_{t}^{t_N} q(\mathbb{x}, \tau) \mathbb{d}\tau$의 합으로 정의한다. 이때, 자유 에너지 함수(Free Energy Function)를 0이 아닌 실수 $\nu \in \mathbb{R}^{\neg 0}$를 도입해 지수 평균의 log를 취한 형태로 정의한다. 여기서, $\rho > 0$은 리스크 회피(Risk Sensitive)를, $\rho < 0$은 리스크 선호(Risk Seeking)을 유도한다.
\[\begin{align} \mathcal{J} & = \mathcal{J}(\mathbb{x}(\cdot), t) = \phi(\mathbb{x}(t_N), t_N) + \int_{t}^{t_N} q(\mathbb{x}, \tau) \mathbb{d}\tau \cdots (26)\\ \xi(\mathbb{x}, t) & = \frac{1}{\rho} \log_e \mathbb{E_P} \biggl[ \exp \left( \rho \mathcal{J}(\mathbb{x}, t) \biggr) \right] \cdots (27) \end{align}\]한편, 이제 시스템에 대한 내용을 도입해 보자. 우리가 제어 입력을 통해 관찰가능한 시스템의 분포를 $\mathbb{Q}$, 아무런 제어 없이 관찰가능한 시스템의 분포를 $\mathbb{P}$라고 해보자. 이때, $\mathbb{w}$는 브라운 노이즈(Brownian Noise) 항이다.
\[\begin{align} \mathbb{P}^{\mathbf{Controlled}}: \mathbb{dx} & = \mathbf{F} \mathbb{(x,u)} \mathbb{d}t + \mathbf{C} \mathbb{(x)} \mathbb{dw}(t) \\ \mathbb{Q}^{\mathbf{Uncontrolled}}: \mathbb{dx} & = \mathbf{A}\mathbb{(x)} \mathbb{d}t + \mathbf{C} \mathbb{(x)} \mathbb{dw}(t) \end{align} \cdots (29)\]먼저, $\delta F$를 다음과 같이 정의하자:
\[\delta \mathbf{F} \mathbb{(x,u)} = \mathbf{F} \mathbb{(x,u)} - \mathbf{A} \mathbb{(x)} = \mathbf{F} \mathbb{(x,u)} - \mathbf{F} \mathbb{(x,0)},\ \forall x, u\]그러면, $\Sigma_\mathbf{C} = \mathbf{C}\mathbb{(x)}\mathbf{C}\mathbb{(x)}^T$라고 정의했을 때 두 확률 변수의 라돈-니코딤 도함수(Radon-Nikodym Derivative)는 다음과 같이 정의할 수 있다:
\[\mathbb{\frac{dQ}{dP}} = \exp \biggl[ \int_{t_0}^{t_N} \left( \delta \mathbf{F}^T\mathbf{C}\mathbb{(x)}^{-1}\mathbb{dw(t)} + \frac{1}{2}\delta \mathbf{F}^T\mathbb{\Sigma}_\mathbf{C}^{-1}\delta \mathbf{F} \delta t \right) \biggr] \cdots (30)\]앞서 소개한 수식 (25)의 르장드르 부등식과 등호 조건에 수식 (30)의 라돈-니코딤 도함수를 적용해보자. 그러면 이 등호식은 $\mathbb{Q}$의 관점에서 상태에 대한 비용인 상태 비용(State Cost)과, 실제 물리적 과정에 따른 $\mathbb{P}$와의 쿨백-라이불러 발산(Kullback-Leibler Divergence)을 의미하는 정보 비용(Information Cost)의 두 항으로 쪼개어 나타낼 수 있다. 더욱이 이 두 비용의 상충 관계(Trad-Off) 중에서 이 둘 모두를 최소화하도록 설계되었다는 점을 확인할 수 있다.
\[\begin{align} - \frac{1}{|\rho|} \log_{e} \mathbb{E_P} \left[ \exp(-|\rho|\mathcal{J}) \right] & \leq \underbrace{\mathbb{E_Q}\left[(\mathcal{J})\right]}_{State\ Cost} + \underbrace{\mathbb{E_Q}\left[\frac{1}{2|\rho|} \delta \mathbf{F}^T\mathbb{\Sigma}_\mathbf{C}^{-1}\delta \mathbf{F} \delta t \right]}_{Information\ Cost} \\ & = \mathbb{E_Q}\left[(\mathcal{J})\right] + \mathbb{E_Q}\left[\frac{1}{2|\rho|} \delta \mathbf{F}^T\mathbb{\Sigma}_\mathbf{C}^{-1}\delta \mathbf{F} \delta t \right],\ when\ \mathbb{dQ^*} = \frac{\exp(- |\rho| \mathcal{J}) \mathbb{dP}}{\int {\exp(- |\rho| \mathcal{J}) \mathbb{dP}} } \end{align} \cdots (31)\]4.3 sHJB 방정식 유도
수식 (29)에서 제어 동역학이 입력에 대해 선형적이라는 어파인(Affine Transformation) 가정을 도입하자.
\[\begin{align} \mathbb{P}^{\mathbf{Controlled}}: \mathbb{dx} & = \mathbf{f} \mathbb{(x)} \mathbb{d}t + \frac{1}{\sqrt{|\rho|}}\mathcal{B} \mathbb{(x)} \mathbb{dw}^{(0)}(t) \\ \mathbb{Q}^{\mathbf{Uncontrolled}}: \mathbb{dx} & = \mathbf{f} \mathbb{(x)} \mathbb{d}t + \mathcal{B} \mathbb{(x)} \biggl( \mathbf{u} \mathbb{d}t + \frac{1}{\sqrt{|\rho|}}\mathbb{dw}^{(1)}(t) \biggr) \end{align} \cdots (32)\]그러면, 자유에너지에 적용된 르장드르 부등식은 다음과 같아진다.
\[\begin{align} \xi(\mathbb{x}) & = - \frac{1}{\rho} \log_e \mathbb{E_P} \biggl[ \exp \left( - |\rho| \mathcal{J}(\mathbb{x}) \biggr) \right] \\ & \leq \mathbb{E_P} \biggl[ \mathcal{J}(\mathbb{x}) + \frac{1}{2} \int_{t_i}^{t_N} \mathbf{u}^T\mathbf{u} \mathbb{d}t \biggr] \end{align} \cdots (33)\]이 때, 다음과 같이 새로운 변수 $\Phi$를 도입해보자.
\[\mathbf{\Phi}(\mathbb{x}, t) = \mathbb{E_P}\left( \exp (\rho \mathcal{J}(\mathbb{x})) \right) \cdots (34)\]그러면, 파인만-칵 공식(Feynman-Kac Formula)에 의해, 이 함수는 콜모고로프 역향 방정식(Kolmogorov Backward Equation)을 따른다. 더욱이 다음의 방정식이 참이다.
\[- \partial_t \mathbf{\Phi} = \rho q_o \mathbf{\Phi} + \mathbf{f}^T(\nabla_\mathbb{x} \mathbf{\Phi}) + \frac{1}{2|\rho|} \mathrm{Tr} \biggl( (\nabla_{\mathbb{xx}} \mathbf{\Phi}) \mathcal{B} \mathcal{B}^T \biggr) \cdots (35)\]앞서 경로 적분 프레임워크에서 활용한 Log 변환과 유사하게 $\mathbf{\xi}(\mathbb{x}) = \frac{1}{\rho} \log \mathbf{\Phi}(\mathbb{x}, t)$를 적용해 수식을 적용하면, 다음과 같은 식이 나온다. 이때, $\rho$의 양수/음수 여부에 따라 동순으로 다음과 같이 정리할 수 있다.
\[- \partial_t \mathbf{\xi} = q_0 + (\nabla_\mathbb{x}\mathbf{\xi})^T \pm \frac{1}{2} (\nabla_\mathbb{x} \mathbf{\xi})^T \mathcal{B}\mathcal{B}^T(\nabla_\mathbb{x} \mathbf{\xi}) + \frac{1}{2|\rho|} \mathrm{Tr} \biggl( (\nabla_{\mathbb{xx}} \mathbf{\xi}) \mathcal{B} \mathcal{B}^T \biggr) \cdots (36)\]그런데, 이 방정식은 바로 sHJB 방정식이다. 이로써, 어떠한 최적성의 원리(Principle of Optimality)를 도입하지 않고도 sHJB을 유도해낼 수 있게 되었다!
이로써, 우리는 복잡한 최적 제어의 문제가 어떻게 확률적 추론의 문제와 관련되는지 수학적으로 살펴 보았다. 1에서는 고전적인 결정론적 최적 제어 문제와 HJB 방정식, 동적 프로그래밍을 활용한 계산 방법을, 2에서는 확률적 최적 제어 문제의 형식화와 sHJB 방정식을 소개했다. 3에서는 확률적 최적 제어 문제를 콜모고로프 역향 방정식으로의 유도한 이후 파인만-칵 공식을 활용한 샘플링 기반의 계산 방법을, 4에서는 확률적 추론의 관점에서 자유 에너지의 개념과 그것의 최소화를 통해 최적성 원리의 가정 없이 sHJB 방정식을 유도해냈다. 바로 이 주제를 통해, 미분 방정식의 재귀적 연산이 확률적 추론과 순방향 샘플링과 연결되는 순간을 포착할 수 있었다.


Comments